The Birthday Problem
The “Birthday Problem” is a classic in introductory probability theory, and it never fails to impress the newly initiated. The problem goes like this:
How many people do you need to have in one room for the probability that at least 2 people in that room share a birthday to be 50%?
The answer may surprise you. Before we get to the answer though, let’s go real briefly into the math behind it.
The probability that two people in a group of \(N\) people share a birthday is the inverse of the statement that everybody in the room has a unique birthday. Both of these cannot be true, and if one of these statements is false, the other must be true. Therefore, if we find the probability of one of these statements (call that probability \(p\) ), the probability of the other is \(1 - p\) . Therefore, we can find the probability that at least 2 people share a birthday by finding the probability that everyone in that room has a unique birthday, and subtracting that number from 1. Following so far?
So what is the probability that in a room of \(N\) people, everyone has a unique birthday? Let’s do an example where we have only 5 people. There are 366 possible birthdays (including February 29), so the first person in this group of 5 people can have any of those 366 birthdays, which we represent as a fraction:
\[ P(\text{Unique birthday with 1 person}) = \frac{366}{366} = 1\]This can be read in English as “The probability that someone has a unique birthday in a group of 1 people is 100%”. This is obvious: if there is only one person, then they of course have a “unique” birthday, since there is no one else in the room to have the same birthday as them.
The 2nd person in the room can have any day as their birthday except the same day as the first person, so there are 365 options for Person 2’s birthday. Therefore, if we have 2 people, the probability that they have different birthdays is
\[ P(\text{Unique birthdays with 2 people}) = \frac{366}{366} \cdot \frac{365}{366} = 0.997\]This pattern continues for every additional person. Therefore, in the event that we have 5 people in a room, the probability that they all have different birthdays is
\[ P(\text{Unique birthdays with 5 people}) = \frac{366}{366} \cdot \frac{365}{366} \cdot \frac{364}{366} \cdot \frac{363}{366} \cdot \frac{362}{366} = 0.973\]Hopefully you’re beginning to see a pattern here.
Now, to find the probability that, in a room of 5 people, at least 2 of them have the same birthday (that is, there are not all unique birthdays), we simply subtract the number above from 1
\[ \begin{aligned} & P(\text{2 or more people have the same birthday}) \\ &= 1 - P(\text{Unique birthdays with 5 people}) = 0.027 \end{aligned}\]As you might expect, this number is pretty small (about 2.7%). So how many people do we need to have in a room in order for there to be a 50% chance that at least 2 people share a birthday?
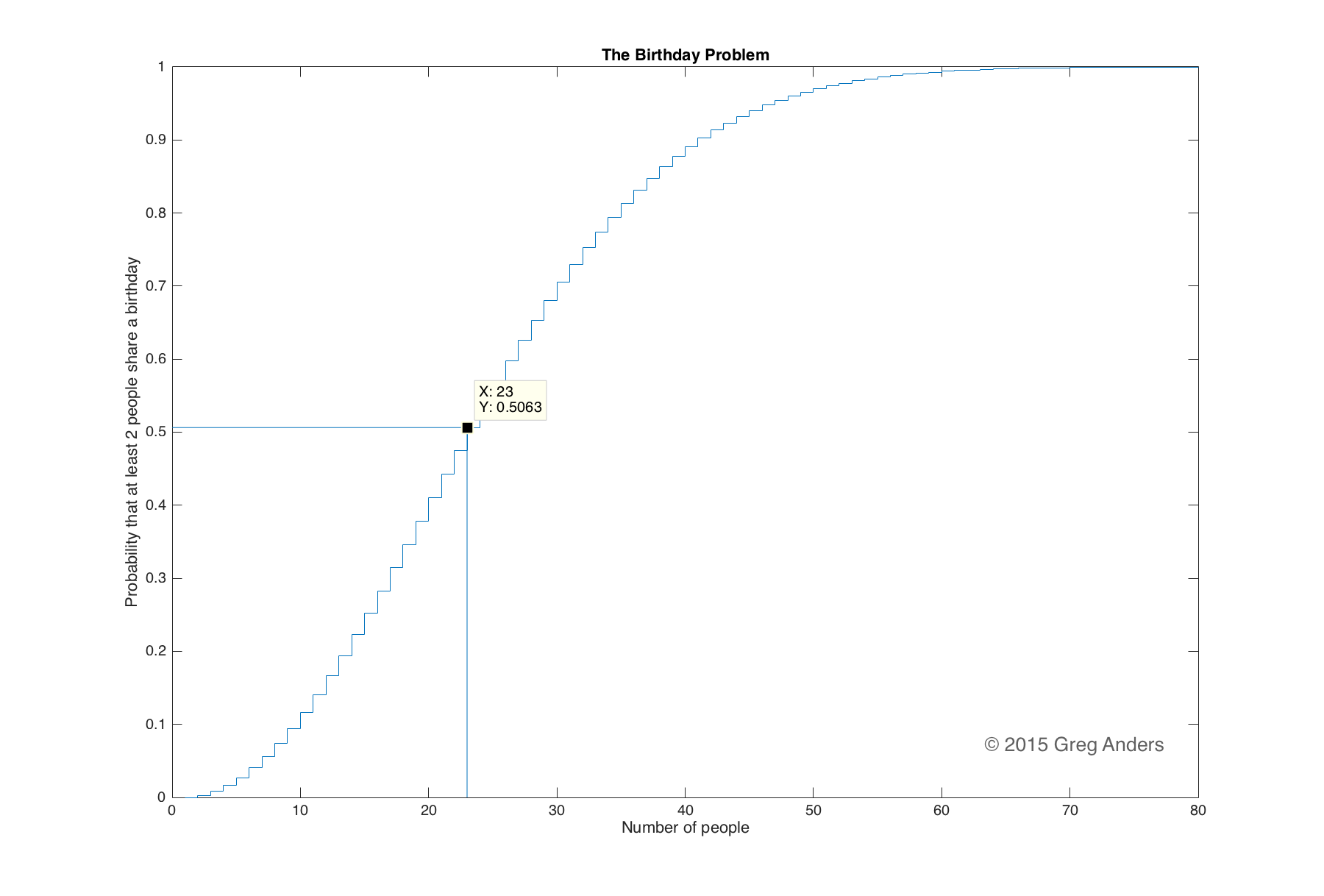
The answer is 23.
Surprising, I know. That seems way too low, and you’re probably a little incredulous. But the math checks out. In fact, it gets even stranger. At 23 people, there is (roughly) a 50% chance that 2 people share a birthday; by the time we get to 50 people the probability is 97%, and by the time we have a room full of 70 people it is a near certainty that at least 2 people will share a birthday (it is only a near certainty: in order to have a mathematical, 100% certainty that 2 people in a group will have the same birthday, you must have at least 367 people).
Looking at the graph below, you’ll see that the probability creeps up slowly until it gets to around 10 people, where it begins to climb rapidly and then taper off again around 40.
For the mathematically inclined, the formula used to calculate this is
\[ 1 - \frac{1}{366^N}\frac{366!}{(366-N)!}\]So, next time you’re in a room with 23 or more people, test the math for yourself and see if anyone shares a birthday - and bonus points for you if you can casually drop the phrase “probability theory” into your conversation.